Simulation of a Vestibular Implant

type

status

date

slug

summary

Background

**Figure 1: A diagram of the vestibular system.**

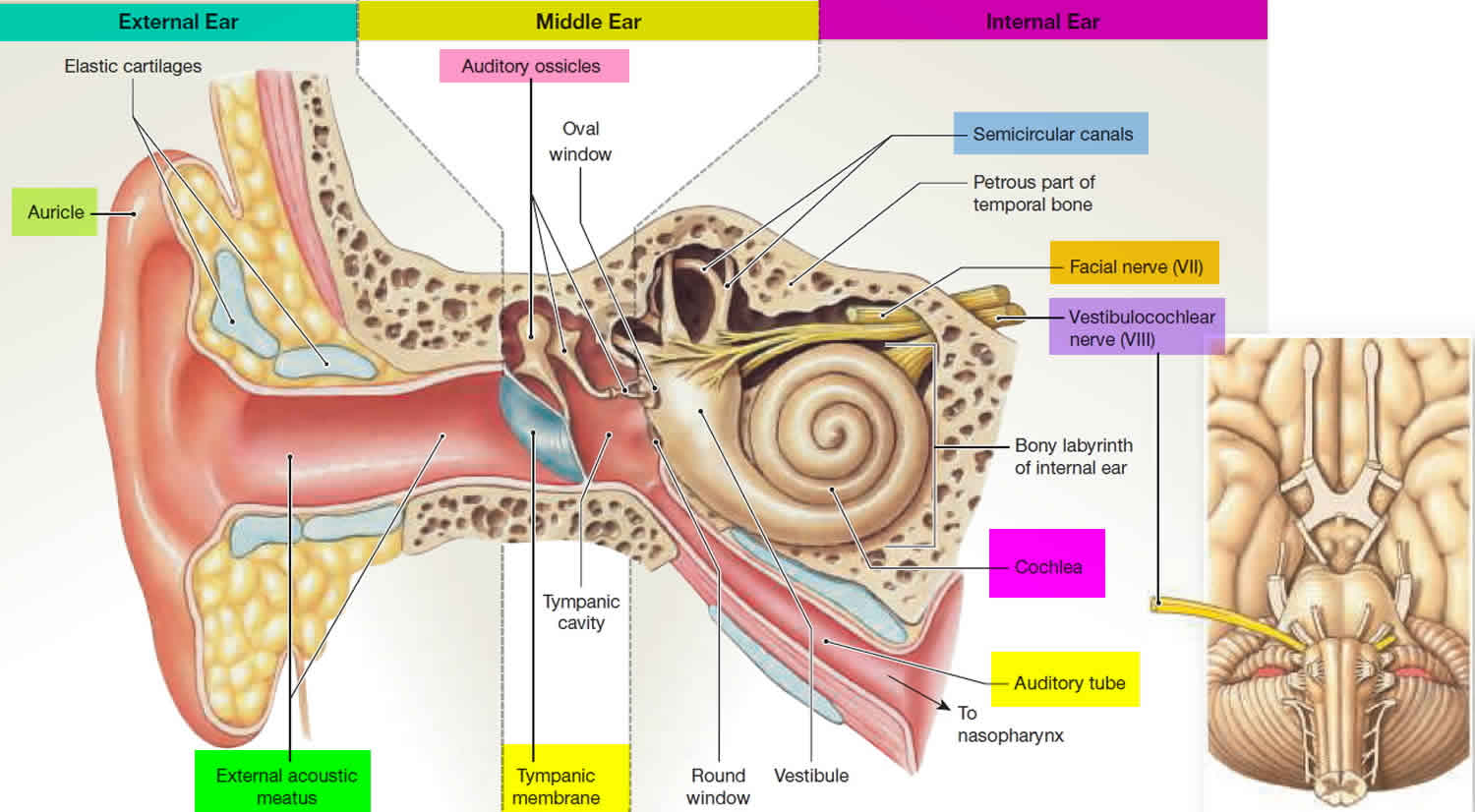
The vestibular system is a sensory system that is critically important in humans for gaze and image stability as well as postural control. Patients with complete bilateral vestibular loss are severely disabled and experience a poor quality of life. There are very few effective treatment options for patients with no vestibular function. Over the last 10 years, rapid progress has been made in developing artificial 'vestibular implants' or 'prostheses', based on cochlear implant technology. As of 2019, 19 patients worldwide have received vestibular implants and the results are encouraging. Vestibular implants are now becoming part of an increasing effort to develop artificial, bionic sensory systems.

Exercise Description: Simulation of a Vestibular Implant

Data

The files Walking_01.txtand Walking_02.txtcontain the linear accelerations and angular velocities recorded when walking in a figure-of-eight, around a table and a chair.

Methods

For measuring the movement a sensor by XSens was used, with the orientation on the head as indicated in the figure below.

At the start of the recordings, the subject was stationary, and the head was in an orientation with Reid's line 15 deg nose up.The sensor orientation on the head is such that at t=0, the "shortest rotation that aligns the y-axis of the sensor with gravity" brings the sensor into such an orientation that the (x/ -z / y) axes of the sensor aligns with the space-fixed (x/y/z) axes. This requirement uniquely determines the sensor-orientation at t=0.

Data were sampled at 50 Hz.

The acceleration data are given in m/s2, the angular velocity data in rad/s.

**Figure 2: A diagram of the walking process and the settings of coordinate systems.**

Task 1: Simulate the vestibular neural response

Simulate the neural vestibular responses during walking, using only the 3D-linear-acceleration and the 3D-angular-velocity from the file Walking_02.txt:

Right horizontal semicribular canal

Calculate the maximum cupular displacements (positive and negative). These two values should be written into the text file CupularDisplacement.txt.

Otolith haircell

Assume that an otolith hair-cell has at t=0 the on-direction=[0 1 0] in space fixed coordinates (i.e. pointing to the left as seen from the subject). Calculate the minimum and maximum acceleration along this direction, in m/s^2 and write this value to the text file MaxAcceleration.txt.

Task 2: Calculate the “nose-direction” during the movement

Calculate the orientation of the “Nose”-vector (as indicated in the figure) at the end of walking the loop (for Walking_02.txt),

based on the angular velocity readings,

and assuming that at t=0: nose=[1,0,0].

Input data

The folder MovementData contains the following files:

Walking_01.txt, Walking_02.txt: Linear acceleration and angular velocity recordings from human subject while walking around.

SCC_Humans.m: Orientations of the human semicircular canals, with respect to "Reid's plane". (Reid's plane is the plane defined by the lower rim of the orbia, and the center of the external auditory meatus. In "English": the bottom of the eyes, and the middle of the ears.)

Tips

Parameters

The radius of the human semicircular canals is 3.2 mm.

For the given input, the magnitude of the cupular displacement is about +/- 0.12 mm.

For the given input, the magnitude of the maximum acceleration along this axis is between -5.63 m/s^2 and +6.87 m/s^2

Implementation

In the implementation, we divide the simulation into two parts: Task 1 and Task 2.

Read in the data

Before implementing the simulations of task 1 and task 2, we need to read in the movement data.


# Load sensor data
dir_data = os.getcwd()
data_sensor = XSens(os.path.join(dir_data, 'MovementData', 'Walking_02.txt'))

Task 1

We set the parameters according to the suggestions in the document of requirements. To make the parameter setting more modularized, we set the parameters in a YAML file and create a class to structurally contain the parameters. The parameter settings are:

What’s more, we also create a graphical interface to allow the users change the parameters interactively.

In task 1, we need to finish two parts of simulations:

Calculate the maximum cupular displacements.

Calculate the minimum and maximum acceleration along this direction.

Data decomposition

In this process, the pre-loaded data is decomposed and some parameters are calculated.


## Data decomposition
acc = data.acc  #  Acceleration
omega = data.omega  #  Angular velocity
rate = data.rate  #  Sample rate
N = data.totalSamples  #  Number of samples

## Parameter calculation
vec_g_hc = np.array([0, 0, -0.981])  #  Gravity in Zurich. Head coordinates.
vec_g_approx = np.dot(sk.rotmat.R(axis='x', angle=90), vec_g_hc)
vec_ref = acc[0, :]  #  Take acc(t=0) as the reference vector.

Calculate the cupular displacement

With the input data and parameters, we can compute the cupular displacement. First, we need to adjust the original angular velocity data from the sensor coordinate system into the head coordinate system. Then, we compute the orientation of the SCCs of humans’ right canal and multiply it with the adjusted angular velocities. The result is the stimulation. Finally, we can calculate the cupular displacement using the stimulus, sampling rate, number of total samples and the radius of SCCs.


## Displacement of the cupula
# Adjust the angular velocities.
omega_adjusted = alignment(data=omega, vec_ref=vec_ref, vec_g=vec_g_approx)
# Orientation of the SCCs in humans.
canal_left, canal_right = sccs_humans()
# Calculate the stimulation using the dot product.
stimulus = np.dot(omega_adjusted, canal_right[0, :])
# Calculate deflection
deflection_cupula = cal_deflection(stimulus, rate, N)
# Calculate displacement
radius_canal = 3.2  #  Radius of the SCC
displacement_cupula = deflection_cupula * radius_canal

The acceleration data can be calculated by adjusting the original acceleration data into the head coordinate system. The otolith acceleration is in the on-direction [0,1,0].


## Acceleration along the on-direction [0 1 0] in the Head coordinates.
# Adjust the acceleration.
acc_adjusted = alignment(data=acc, vec_ref=vec_ref, vec_g=vec_g_approx)
# Preserve the component in the on-direction [0, 1, 0].
acc_otolith = acc_adjusted[:, 1]

Preserve the results

We save the results of task 1 locally. For simplicity, we only preserve the maximum and minimum data.


## Write the values in text files.
# Cupular Displacement
path_cupular = os.path.join(dir_crt, 'output/CupularDisplacement.txt')
with open(path_cupular, 'w', encoding='utf-8') as f:
    f.writelines(f'Maximum cupular displacement (positive): \
                 {np.max(displacement_cupula)} mm\n')
    f.writelines(f'Maximum cupular displacement (negative): \
                 {np.min(displacement_cupula)} mm\n')
print('The maximum cupular displacements have been saved to: ')
print(path_cupular)
# Acceleration
path_acc = os.path.join(dir_crt, 'output/MaxAcceleration.txt')
with open(path_acc, 'w', encoding='utf-8') as f:
    f.write(f'Maximum acceleration along the direction of the otolith hair cell: \
            {np.max(acc_otolith)} m/s^2\n')
    f.write(f'Minimum acceleration along the direction of the otolith hair cell: \
            {np.min(acc_otolith)} m/s^2\n')
print('The maximum and minimum acceleration have been saved to: ')
print(path_acc)

Task 2

In task 2, we need to finish two parts of simulations:

Calculate the “nose-direction” during the movement.

Visualize the quaternions to describe the head orientation.

Caculate the nose orientation

In order to calculate the nose orientation, we need to get the head orienation. In the head coordinate system, we can rotate the angular velocities according to the relative pose of the Reid’s line and use quaternions to compute the head orientation. The nose orientation can then be computed based on the head orientation and the fact that “at t=0: nose=[1,0,0]”.


# Head orientation
orientation_head = cal_head_orientation(omega_adjusted)
    
# Nose orientation
orientation_nose = []
for i in range(orientation_head.shape[0]):
    R_tmp = sk.quat.convert(orientation_head[i, :], to='rotmat')
    # t=0: nose=[1 0 0]
    orientation_nose.append(np.matmul(R_tmp, np.array([1,0,0])))
orientation_nose = np.array(orientation_nose)

# Write the values in text files.
path_nose_dir = os.path.join(dir_crt, 'output/Nose_end.txt')
with open(path_nose_dir, 'w', encoding='utf-8') as f:
    f.write(f'The orientation if the "Nose"-vector at the end of the walking loop: \
            {orientation_nose[-1]} m/s^2\n')
print('The nose vector at the end of the walking loop has been saved to:')
print(path_nose_dir)

Visualize the head orientation

The head orientation is represented in the form of quaternions. We can visualize the head orientation at each moment using a curve graph.


# Visualization of the head orientation
plt.plot(np.linspace(0, 20, orientation_head.shape[0]), orientation_head[:, 1], color='blue')
plt.plot(np.linspace(0, 20, orientation_head.shape[0]), orientation_head[:, 2], color='green')
plt.plot(np.linspace(0, 20, orientation_head.shape[0]), orientation_head[:, 3], color='red')
plt.grid(linestyle='--')
plt.xlim([0, 20])
plt.ylim([-0.4, 1.0])
plt.title('Head Orientation')
path_img = os.path.join(dir_crt, 'output', 'head_orientation.PNG')
plt.savefig(path_img)
print('The visualization result of the head orientation has been saved to:')
print(path_img)

3D visualization of the nose orientation

After computing the nose orientation, we visualize the 3D process of the movement. We save the simulation result as a GIF file. In the implementation, we write a seperate function to reconstruct the 3D process.


def visualization_nose(orientation_nose, dir_crt):
    """3D visualization of the nose orientation.

    Parameters
    ----------
    orientation_nose: Nose orientations during the movements.
    dir_crt: Directory of the current folder.

    Returns
    -------
    
    """

    fig = plt.figure()
    # Initialize the 3D coordinates.
    ax = fig.add_subplot(projection='3d')
    # Visualize the nose vectors dynamically.
    x = np.linspace(-1, 1, 5)
    y = np.linspace(-1, 1, 5)
    X, Y = np.meshgrid(x, y)
    for i in range(len(orientation_nose)):
        # Progress meter
        PSG.one_line_progress_meter(
            'Video frame generating.',
            i+1,
            len(orientation_nose),
            '',
            'Generating frames of the nose orientation...'
        )
        # Clear the current figure.
        plt.cla()
        # 3D surfaces for better visualization
        ax.plot_surface(X, Y, Z=X*0, color='g', alpha=0.2)
        ax.plot_surface(X, Y=X*0, Z=Y, color='y', alpha=0.2)
        ax.plot_surface(X=X*0, Y=Y, Z=X, color='r', alpha=0.2)
        # Plot a 3D arrow (Nose).
        vec_tmp = orientation_nose[i]
        ax.quiver(0, 0, 0, 
                  vec_tmp[0], vec_tmp[1], vec_tmp[2], 
                  arrow_length_ratio=0.2, color='black', normalize=True)
        # Plot settings
        ax.set_xlabel('x')
        ax.set_ylabel('y')
        ax.set_zlabel('z')
        ax.set_xlim(-1.0, 1.0)
        ax.set_ylim(-1.0, 1.0)
        ax.set_zlim(-1.0, 1.0)
        plt.title('myNose ' + str(i) + '/' + str(len(orientation_nose)))
        path_tmp = os.path.join(dir_crt, 'output', '3D_tmp', str(i)+'.PNG')
        plt.savefig(fname=path_tmp)
    # imageio
    gif_images = []
    for i in range(len(orientation_nose)):
        # Progress meter
        PSG.one_line_progress_meter(
            'GIF generating.',
            i+1,
            len(orientation_nose),
            '',
            'Generating the GIF of the nose orientation...'
        )
        # GIF images
        path_tmp = os.path.join(dir_crt, 'output', '3D_tmp', str(i)+'.PNG')
        gif_images.append(imageio.imread(path_tmp))
    
    # Save the output
    path_save = os.path.join(dir_crt, 'output', 'myNose.gif')
    imageio.mimsave(path_save, gif_images, fps=50)
    print('The GIF which shows the nose orientation has been saved to:')
    print(path_save)

Demo

Here we present some results of this simulation task. The running time often takes 1-2 minutes (most of the time is used by 3D visualization).

**Figure 3: The head orientation during the moving process.**

**Figure 4: 3D visualization of the nose orientation.**

The complete source code can be found in my GitHub.